Absolute Maximum Shear Stress Equation

Maximum shear stress theory provides failure criteria of mechanical components made of a ductile textile. This failure criterion is adult by the French mechanical engineer, Henri Tresca and based on his name maximum shear stress theory is also known as the Tresca theory of failure. Due to the enormous contribution in the field of plasticity, Henry Tresca is popular as the father of the field of plasticity.

Maximum shear stress theory is one of the 2 main failure criteria that are widely used in contempo times for predicting the failure of ductile materials. To establish failure criteria of material, all failure theories compare a specific parameter with the same parameter for the uniaxial tension test. The maximum shear stress theory is no exception and the parameter for comparison in Tresca theory is maximum shear stress.

"The maximum shear stress theory states that the failure or yielding of a ductile material will occur when the maximum shear stress of the fabric equals or exceeds the shear stress value at yield point in the uniaxial tensile test."

Maximum shear stress theory formula

Let's deduce the mathematical form of the above-mentioned Tresca theory argument.
Considering main stresses, at the yield point, the main stresses in a uni-centric test, σ₁ =σ_y; σ_two = 0 and σ₃ = 0.
And so the maximum shear stress at yielding: σ_sy =σ_ane/2. Therefore σ_sy = σ_y/ii

Now assuming σ₁ >σ₂ >σ₃; the maximum shear stress for the fabric is given by:

τ_max=(σ₁ -σ₃ )/two

Now comparing these to maximum shear stresses following Tresca theory, failure will happen when τ_max>=σ_sy

Rubber Design Condition as per Tresca theory of failure

So the blueprint of a mechanical component should be based on the post-obit maximum shear stress theory equation

τ_max<=σ_sy or (σ_one -σ₃ )<=σ_y

The gene of condom (N) tin can also be calculated based on maximum shear stress theory and given by N=σ_sy /τ_max

Hence, maximum permissible shear stress for designing a component equally per maximum shear stress theory is given by τ_max =σ_sy /Northward

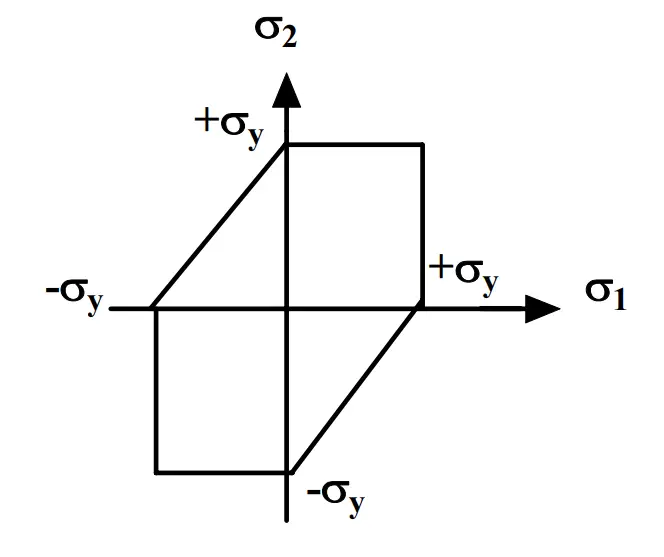
The failure envelope for Tresca theory of failure is provided in Fig. 1 below:

**Fig. 1: Failure Envelope as per Maximum Shear Stress Theory**

Steps for using the Maximum Shear Stress Theory

To utilise the maximum shear stress theory in trouble solving the post-obit steps are necessary to be followed:

Footstep ane: Determine the three principal stresses (σ₁,σ2, and σ3) from the tri-centric stress system using main stress equations or Mohr'southward circle method.
Step 2: Find out the maximum (σ1) and the minimum (σ3) principal stresses.
Footstep 3: Determine the value of the maximum shear stress τmax=(σ1 -σ3 )/2.
Step 4: Observe out the commanded stress value of the material; commanded stress= σsy /N or σy /2N as mentioned to a higher place (Northward=Factor of safety)
Pace 5: Compare the value calculated at step 3 with the allowable value found at pace iv. If the Value at pace 3 is less than the allowable value at pace four, and then the design is safe equally per the maximum shear stress theory.

Maximum Shear Stress Theory vs Von Mises Stress Theory

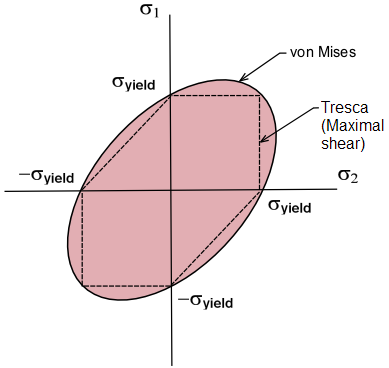
Von Mises and Tresca failure criteria are usually presented jointly with trivial bigotry between them. However, there are a few differences between them which are tabulated below:

Maximum Shear Stress Theory	Von Mises Stress Theory
Maximum Shear Stress theory or Tresca theory of failure relates to the maximum shear stress of ductile materials.	Von Mises stress theory represents the maximum distortion energy of a ductile material.
This theory is considered to exist more than conservative.	Considered less conservative when compared with Tresca theory.
Component cost increases.	Optimized Component Toll.
Required but 2 chief stress equations (σ_max and σ_min) to calculate the maximum shear stress.	Employ all the three primary stresses (σ_one ,σ_ii , and σ₃) in its equation for calculating Von Mises Stress.

Table: Tresca theory vs Von Mises theory

The failure envelope for Tresca theory and Von Mises theory is given in Fig. 2:

**Fig. ii: Failure Envelope as per Tresca and Von Mises Stress Theory**

Limitations of Maximum Shear Stress Theory

The maximum shear stress theory does not give accurate results for the land of pure shear stresses adult past the Torsion test.
The Tresca theory provides bourgeois results leading to an increase in component cost.
This theory is not applicable to brittle materials.