How To Find Ox In Statistics

Contents:

1. What is the Central Limit Theorem?
   • Definition using Calculus
2. Primal Limit Theorem Examples: Footstep past step with video clips
3. Central Limit Theorem on the TI 89
4. TI 83 Central Limit Theorem (video)

What is the Central Limit Theorem?

Lookout the video for an overview:

Central limit theorem less than example two

Can't see the video? Click here.

The Central Limit Theorem states that the sampling distribution of the sample means approaches a normal distribution as the sample size gets larger — no matter what the shape of the population distribution. This fact holds especially true for sample sizes over 30.

All this is saying is that equally you accept more than samples, especially big ones, your graph of the sample means volition look more like a normal distribution.

Here's what the Primal Limit Theorem is saying, graphically. The movie below shows one of the simplest types of test: rolling a off-white die. The more than times you ringlet the die, the more than probable the shape of the distribution of the means tends to look like a normal distribution graph.

Photo credit:cmglee|Wikimedia Commons

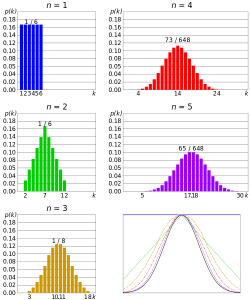
The Fundamental Limit Theorem and Means

An essential component of the Central Limit Theorem is that the average of your sample means will be the population mean. In other words, add up the ways from all of your samples, notice the average and that average will be your actual population hateful. Similarly, if you find the boilerplate of all of the standard deviations in your sample, yous'll find the actual standard divergence for your population. It's a pretty useful phenomenon that tin assistance accurately predict characteristics of a population. Picket a video explaining this miracle, or read more about it here: The Mean of the Sampling Distribution of the Mean.

Definition using Calculus

• X_n is an IID sequence,
• Φ(z) = ℙ (Z ≤ z) =

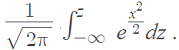
Note: An assumption is that the expected value of X and Ten² < infinity.

Key Limit Theorem Examples

Demand assistance with a homework question? Check out our tutoring page!

A Central Limit Theorem word trouble will nigh probable contain the phrase "presume the variable is usually distributed", or i like information technology. With these cardinal limit theorem examples, you will be given:

1. A population (i.e. 29-yr-old males, seniors between 72 and 76, all registered vehicles, all cat owners)
2. An average (i.e. 125 pounds, 24 hours, 15 years, $15.74)
3. A standard deviation (i.due east. 14.4lbs, 3 hours, 120 months, $196.42)
4. A sample size (i.e. xv males, x seniors, 79 cars, 100 households)

Click the link to skip down to one of three primal limit theorem examples:

• I want to find the probability that the mean is greater than a certain number
• I want to notice the probability that the mean is less than a certain number
• I want to find the probability that the mean is between a certain fix of numbers either side of the mean

Primal Limit Theorem Examples: Greater than

For Primal Limit Theorem give-and-take problems that contain the phrase "greater than" (or a similar phrase such equally "above").

Scout the video for an case.

Central Limit Theorem Greater Than Example #3

Tin can't see the video? Click here.

1. General Steps
Step one: Identify the parts of the trouble. Your question should state:

1. the hateful (boilerplate or μ)
2. the standard difference (σ)
3. population size
4. sample size (north)
5. a number associated with "greater than" ( ). Note: this is the sample hateful. In other words, the trouble is request you "What is the probability that a sample mean of x items will be greater than this number?

Step 2: Draw a graph. Characterization the middle with the mean. Shade the area roughly above (i.eastward. the "greater than" expanse). This step is optional, but information technology may assistance you meet what you are looking for.

Step 3: Use the following formula to notice the z-score. Plug in the numbers from step i.

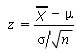
Click hither if you desire easy, step-past-step instructions for solving this formula.

1. Subtract the mean (μ in footstep 1) from the 'greater than' value (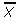in step ane). Set this number aside for a moment.
2. Dissever the standard difference (σ in step i) past the square root of your sample (n in pace 1). For example, if thirty half dozen children are in your sample and your standard deviation is 3, and so 3 / √36 = 0.5
3. Split your event from step 1 past your result from step 2 (i.east. step 1/step two)

Step four: Look upwardly the z-score you calculated in step three in the z-tabular array. If you don't recollect how to expect up z-scores,  yous can find an explanation in pace 1 of this article: Area to the right of a z-score.

Stride v: Subtract your z-score from 0.5. For example, if your score is 0.1554, then 0.5 – 0.1554 = 0.3446.

Stride half-dozen: Convert the decimal in Step v to a percentage. In our example, 0.3446 = 34.46%.

That's it!

ii. Specific Example

Q. A sure group of welfare recipients receives SNAP benefits of $110 per week with a standard deviation of $20. If a random sample of 25 people is taken, what is the probability their hateful do good volition be greater than $120 per week?

Step 1: Insert the information into the z-formula:
= (120-110)/xx √25 = 10/ (20/five) = 10/4 = 2.five.
Step 2: Look up the z-score in a table (or summate it using technology). A z-score of two.5 has an area of roughly 49.38%. Adding 50% (for the left half of the bend), nosotros get 99.38%.

Back to top for more Central Limit Theorem Examples

Central Limit Theorem Examples: Less than

Solving Cardinal Limit Theorem word issues that contain the phrase "less than" (or a similar phrase such as "lower").
Sentry the video for a worked example:

Central limit theorem less than example 2

Can't see the video? Click here.

1. General Steps
Step 1: Identify the parts of the trouble. Your question should country:

1. the mean (average or μ)
2. the standard difference (σ)
3. population size
4. sample size (n)
5. a number associated with "less than" ( )

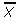Step two: Draw a graph. Label the centre with the mean. Shade the expanse roughly below (i.east. the "less than" area). This step is optional, simply it may help you meet what you are looking for.

Step 3: Use the following formula to notice the z-score. Plug in the numbers from step 1.

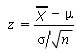
Click hither if you want simple, step-by-pace instructions for using this formula.
If formulas confuse yous, all this formula is request yous to practise is:

1. Subtract the mean (μ in stride 1) from the less than value ( 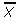in step i). Set this number aside for a moment.
2. Dissever the standard departure (σ in step 1) by the foursquare root of your sample (north in stride i). For example, if 30 six children are in your sample and your standard deviation is ii, and then 3 / √ 36 = 0.5
3. Divide your result from pace 1 past your issue from stride 2 (i.e. footstep 1/step ii)

Footstep 4: Wait upwardly the z-score you calculated in step 4 in the z-table. If you don't remember how to await upward z-scores yous can discover an explanation in step ane of this commodity on area to the right of a z-score in a normal distribution curve.

Step 5: Add your z-score to 0.5. For example, if your z-score is 0.1554, so 0.5 + 0.1554 is 0.6554.

Footstep six: Convert the decimal in Pace 6 to a percentage. In our example, 0.6554 = 65.54%.

That's it!

ii. Specific Case
A population of 29 yr-onetime males has a mean salary of $29,321 with a standard deviation of $ii,120. If a sample of 100 men is taken, what is the probability their mean salaries volition be less than $29,000?

Step one: Insert the values into the z-formula:
= (29,000 – 29,321) / (2,120/√100) = -321/212 = -1.51.

Step ii: Look up the z-score in the left-hand z-table (or use technology). -1.51 has an area of 93.45%.
Withal, this is not the answer, as the question is request for LESS THAN, and 93.45% is the area "greater than" and so you demand to subtract from 100%.
100% – 93.45% = 6.55% or about 0.07.

Back to acme for more Central Limit Theorem Examples

Central Limit Theorem Examples: Between

Watch the video for an example:

Central Limit Theorem Example

Can't run across the video? Click here.

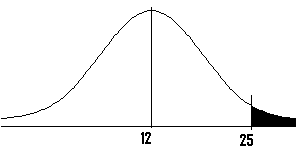
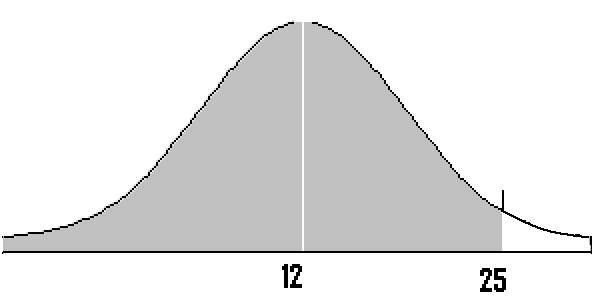
Instance problem: There are 250 dogs at a canis familiaris show who weigh an average of 12 pounds, with a standard deviation of eight pounds. If 4 dogs are chosen at random, what is the probability they have an boilerplate weight of greater than 8 pounds and less than 25 pounds?

Step 1:Identify the parts of the trouble. Your question should land:

• mean (average or μ) standard deviation (σ) population size
• sample size (northward)
• number associated with "less than" 1
• number associated with "greater than" two

Step two: Depict a graph. Label the center with the mean. Shade the surface area betwixt   1 and   2. This stride is optional, but it may help yous see what you are looking for.

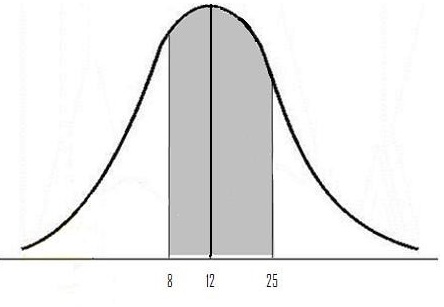
Step three: Use the following formula to find the z-scores.

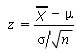
All this formula is request you lot to do is:

a) Subtract the mean (μ in Step 1) from the greater than value (Xbar in Pace 1): 25 – 12 = 13.
b) Split the standard divergence (σ in Step i) by the square root of your sample (n in Step 1): 8 / √ 4 = 4
c) Separate your result from a by your result from b: thirteen / iv = 3.25

Stride 4 Use the formula from Step 3 to observe the z-values. This time, apply Xbar2 from Step 1 (8).

a) Subtract the mean (μ in Step 1) from the greater than value (Xbar in Step 1): viii – 12 = -iv.
b) Divide the standard deviation (σ in Stride 1) by the square root of your sample (n in Step 1): 8 / √ iv = 4
c) Separate your result from a past your result from b: -4 / 4= -i

Step 5: Wait up the value you calculated in Step 3 in the z-table.

Z value of three.25 corresponds to .4994

Step half dozen: Look upward the value you calculated in Stride 4 in the z-tabular array.

Z value of 1 corresponds to .3413

Note that the bong curve is symmetrical, then if you want to look up a negative value like -1, and then just look up the positive counterpart. The area will be the same.

Step vii: Add Stride 5 and 6 together:

.4994 + .3413 = .8407

Step 8: Convert the decimal in Footstep 7 to a percentage:

.8407 = 84.07%

That'due south information technology!
Back to top for more Central Limit Theorem Examples

Central Limit Theorem on the TI 89

Example trouble: A population of community higher students includes inner metropolis students (p = .33). What is the probability that a random sample of 45 students from the population volition take from twenty% to forty% inner city students?

Step i: Press APPS. Highlight the Stats/List Editor by using the scroll keys. Press ENTER.
If you don't see the Stats/List editor you need to load the app. See instructions hither.

Step ii: Press F5 and ringlet downwardly to C: BinomialCdf.

Step three: Enter 45 in the Num Trials box.

Pace 4: Scroll down and enter .33 in the Prob Success box.

Step 5: Ringlet downwardly and enter 9 in the Lower Value box (because twenty% of 45 = 9).

Stride 6: Whorl down and enter 18 in the Upper Value box (because 40% of 45 = xviii). Press ENTER.

Pace 7: Read the Result: Cdf = .857142. This ways that the probability your random sample will have xx – 40% inner city students is 85.71%.

TI 83 Central Limit Theorem: Overview

Watch the video or read the article beneath:

TI 83 Primal Limit Theorem Examples

Can't meet the video? Click hither.

The TI 83 calculator has a congenital in function that can help you calculate probabilities of fundamental theorem word bug, which usually incorporate the phrase "assume the distribution is normal" (or a variation of that phrase).

The function, normalcdf, requires you to enter a lower bound, upper bound, mean, and standard deviation.

Example trouble: A fertilizer visitor manufactures organic fertilizer in 10 pound bags with a standard departure of 1.25 pounds per bag. What is the probability that a random sample of 15 bags will take a hateful betwixt 9 and nine.5 pounds?

Step ane : 2nd VARS 2.

Pace ii : Enter your variables (lower leap, upper leap, hateful, and standard deviation). Separate each variable by a comma: 9,9.5, 10,(1.25/√xv)).

Stride three : Press ENTER. This returns the probability of .05969, or .05969%.

Tip:If yous have a question that asks for "greater than" or "less than" a sure number, enter 999999999 for the lower or upper spring. For example, if you wanted to know the probability of greater than eight pounds y'all would enter:
NORMALCDF(viii,999999999,10,ane./√(15))
Less than 8 pounds you would enter:
NORMALCDF(999999999,8,10,1./√(15))

Tip: Sampling distributions crave that the standard deviation of the mean is σ / √(n), so brand sure you enter that as the standard deviation.

Bank check out our statistics YouTube channel for more tips and key limit theorem examples!

References

Gonick, 50. (1993). The Drawing Guide to Statistics. HarperPerennial.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.

Demand assistance with a homework or exam question? With Chegg Report, you tin go stride-by-step solutions to your questions from an expert in the field. Your showtime 30 minutes with a Chegg tutor is free!

Source: https://www.statisticshowto.com/probability-and-statistics/normal-distributions/central-limit-theorem-definition-examples/

Share this post